[新しいコレクション] 三角比の相互関係の公式 266305-三角比の相互関係の公式 覚え方

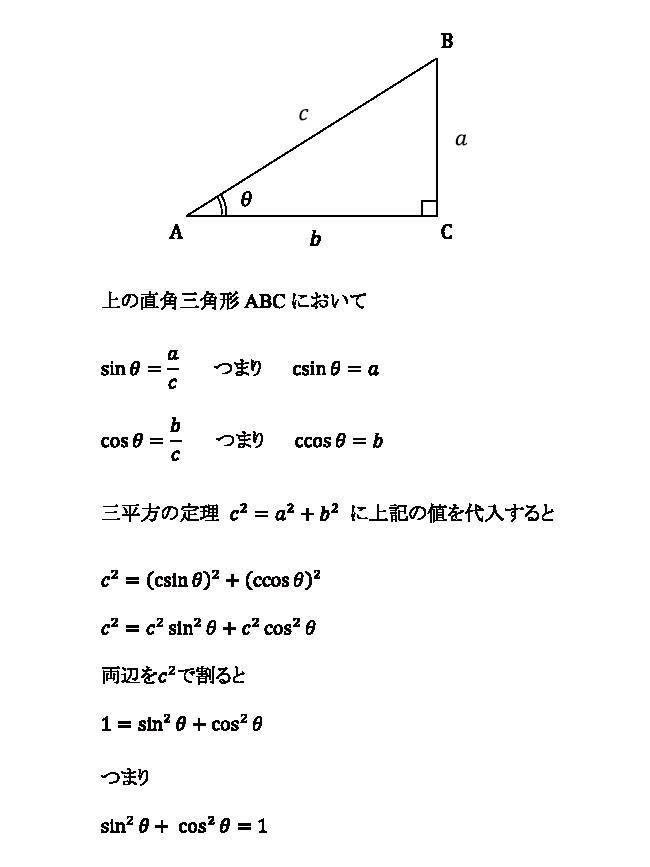
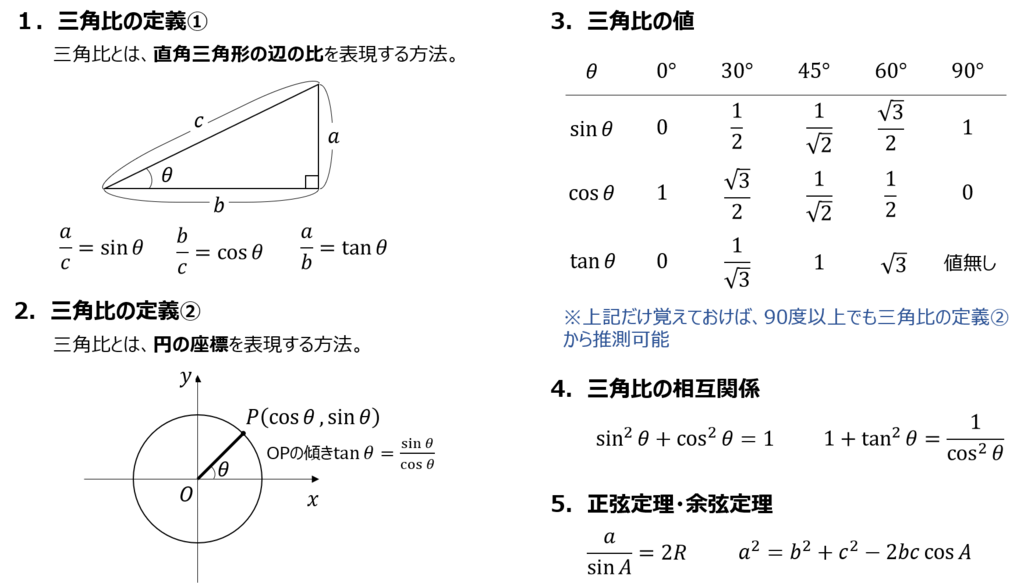
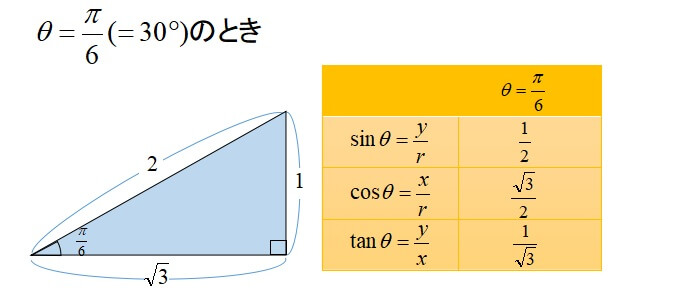
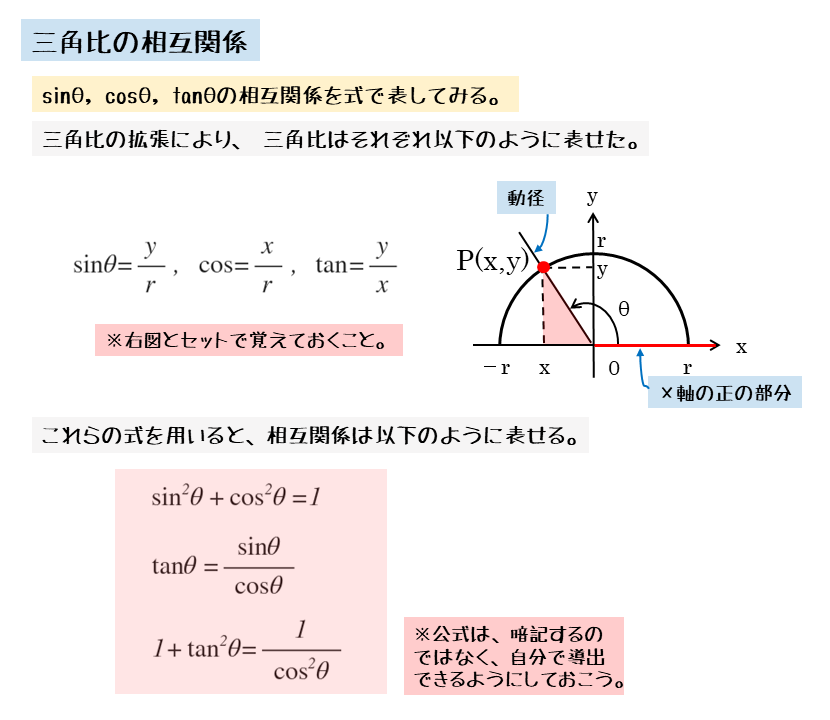
 三角比の重要公式とその証明を解説します。今回解説するのは以下の3つの式です。三角比相互関係の公式！$$\sin^2 θ\cos^2 θ=1・・・(1)$$$$\tan θ=\frac{\sin θ}{\cos θ}・・POINT 公式の1つ目は、 sinθ 2 cos 2 θ＝1 つまり角度が同じθの三角比について、 sinとcosの値をそれぞれ2乗して足すと、必ず1になる わけだね。 公式の2つ目は、 tanθ＝sinθ/cosθ つまり角度が同じθの三角比について、 sinをcosで割ると、tanになる わけだね。 この2つの 重要公式 は 90°を超える範囲でも使える よ。 ただし、90°を超える範囲では cosθとtanθの値がこのページでは、 数学Ⅰの「三角比の公式」をまとめました。 三角比の公式と覚え方を、わかりやすく解説していきます。 数Ⅱの三角関数は「三角関数 公式一覧」で詳しく説明しているので、チェックしてみてください。 問題集を解く際の参考にしてください！

高校数学 連立三角方程式 三角関数の相互関係 合成 加法定理の利用 受験の月

三角比の相互関係の公式 覚え方

三角比の相互関係の公式 覚え方- "三角関数 (三角比)の相互関係"の公式とその証明です！ 三角関数 (三角比)の相互関係公式三角関数の相互関係 \(・sin^2θcos^2θ=1\) \(・tanθ=\frac{sinθ}{cosθ}\) \(・1tan^2θ= なぜ？ 三角関数の相互関係 数学 よく見かけるこの3つの公式 ① tanθ = sinθ cosθ ② sin2θ cos2θ = 1 ③ tan2θ 1 = 1 cos2θ この成り立ちを順に考えましょう。 三角比の確認

高校数学 三角比 使って覚える三角比の基本公式 数学の面白いこと 役に立つことをまとめたサイト

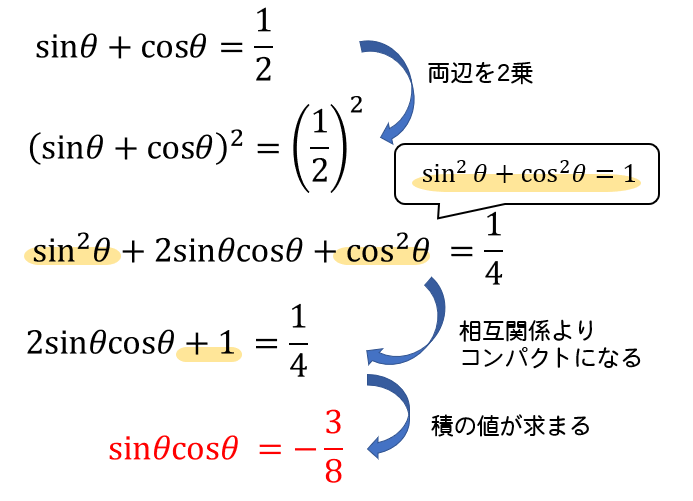
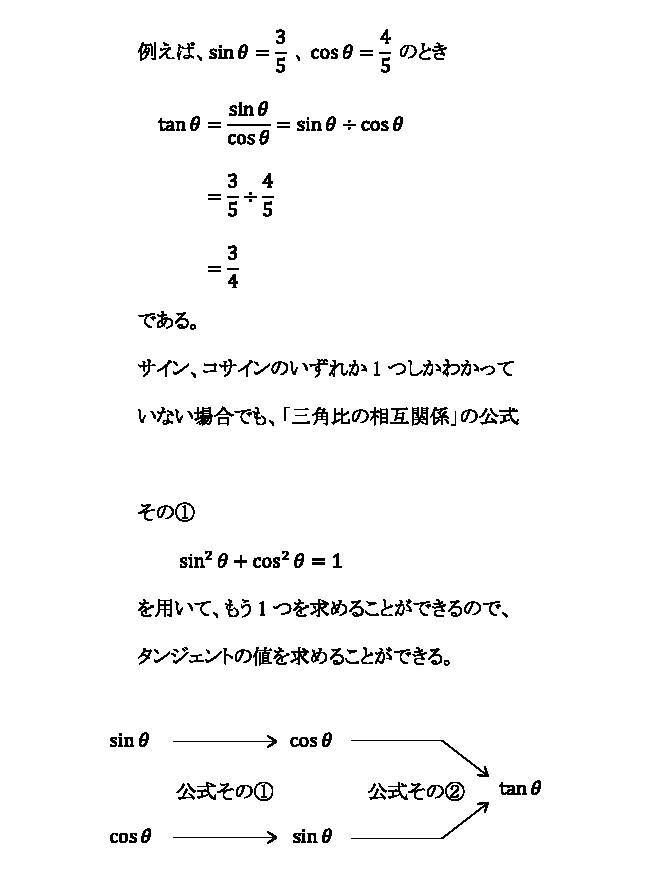
三角比の相互関係は、三角比の1つの値がわかれば、ほかの2つの値がわかる大事な公式です。 例題を解いてみましょう。 cosA＝3／4のとき、sinA まず、cosAからsinAの値を求めるには、三角比の相互関係のどの式を使うと良いか考えます。三角比の相互関係 例題1 例題2 練習問題1 練習問題2 三角不等式 例題 練習問題 sinθ，cosθ，の対称式 例題 練習問題 三角方程式（2次） 例題 練習問題 三角比の2次関数の最大と最小 例題 練習問題 三角比の相互関係 練習問題1 練習問題1 つぎの各場合，他高校数学Iで登場する「三角比の相互関係」とは、次の2つの公式のことです。 sin 2 A cos 2 A=1 (1)

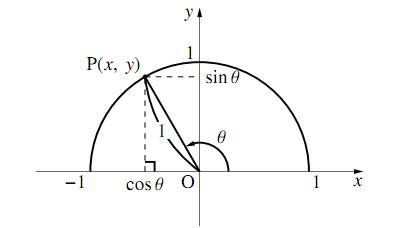
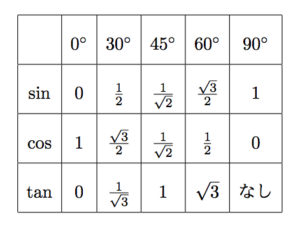
三角比の相互関係 三角比の相互関係として、代表的な 3 3 つの式があります。 必ず暗記しましょう。 sin2 θ cos2 θ = 1 sin 2 ⁡ θ cos 2 ⁡ θ = 1 tan θ = sin θ cos θ tanSway is an easytouse digital storytelling app for creating interactive reports, presentations, personal stories and more Its builtin design engine helps you create professional designs in minutes With Sway, your images, text, videos, and other multimedia all flow together in a way that enhances your story Sway makes sure your creations look great on any screen 以上が、三角比の相互関係とその証明でした。 証明も合わせて覚えておくと、覚え間違いを無くせます。 90º θ, 180º θ, 90º θ の三角比 では続いて、90º θ や 180º θ の三角比の公式を見ていきます。 まずは公式を一通りご紹介しますね。 ＜90º θ＞

三角比の相互関係 sin2θ cos2θ = 1, tanθ = sinθ cosθ○　高校数学Ｉで登場する「三角比の相互関係」とは、次の２つの公式のことです。 sin 2 A cos 2 A=1 (1) 三角比の公式です。 相互関係は実は3つありますが、皆さんがやるのは2つまでです。 大体の場合はサインかコサインがわかっていて、相互関係②に代入してもう片方を求めます。 そのあと、相互関係①に代入してタンジェントを求めます。 別解として、三平方の定理を用いた解き方があ

高校数学 連立三角方程式 三角関数の相互関係 合成 加法定理の利用 受験の月

三角関数の公式 図的理解

公式（三角比 ）－1 － 公式（三角比） 相互関係 tanA = sinA cosA sinA = tanAcosA cosA = sinA tanA cos2 Asin2 A = 1 1tan2 A = 1 cos2 A 1 tan2 A 1 = 1 sin2 A 正弦定理1 a b c = sinA sinB sinC 正弦定理2 a sinA = b sinB =正弦 (sin)半径とy座標の比 余弦 (cos)半径とx座標の比 正接 (tan)x座標とy座標の比 が決まります。 そこで，これら3つの三角比にはどのような関係があるのか求めることにしましょう。 結論を先に述べますと，次の3つが挙げられます。 まとめ2 では，これらの関係を証明してみましょう。 三角比の相互関係つまり角度が同じθの三角比について、 sinとcosの値をそれぞれ2乗して足すと、必ず1になる わけだね。 公式の2つ目は、 tanθ＝sinθ/cosθ

三角比の拡張 数学i フリー教材開発コミュニティ Ftext

高校数学 三角比 使って覚える三角比の基本公式 数学の面白いこと 役に立つことをまとめたサイト

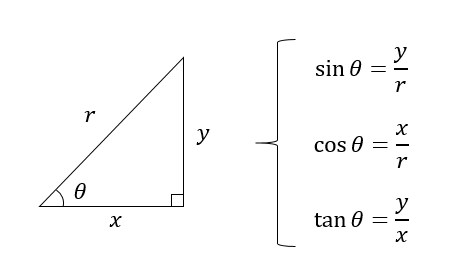
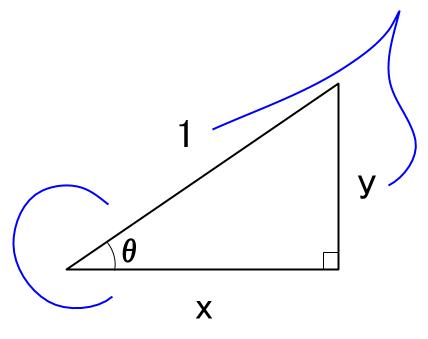
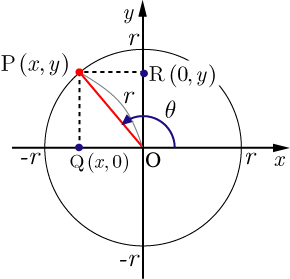
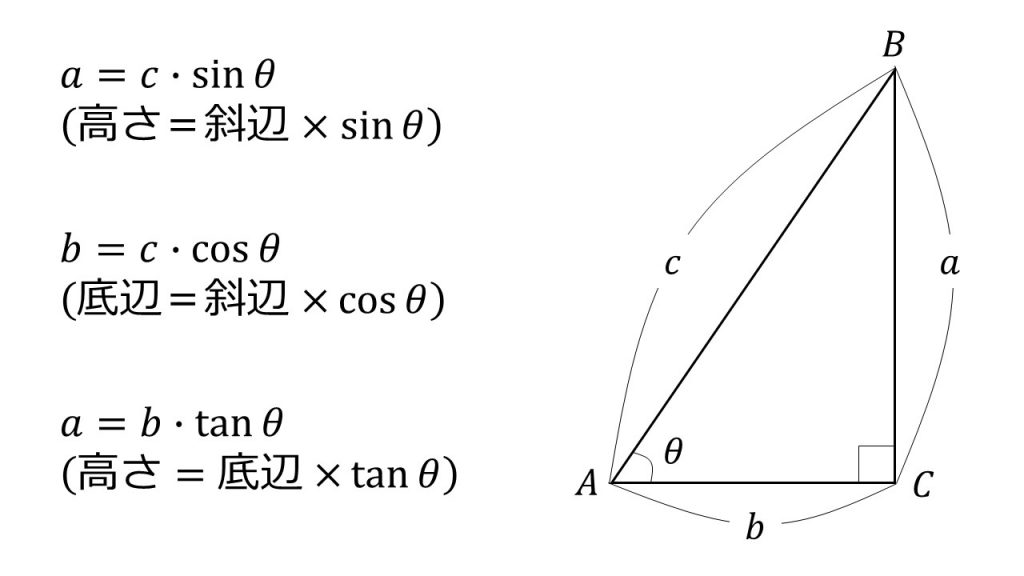
そのためにあるのが、三角比の相互関係の公式です。 tanθ＝sinθ/cosθ sin2θ＋cos2θ＝1 1＋tan2θ＝1/cos2θ (2は指数として読んでください。 三角関数の倍角みたいに見えて嫌なんですけど) この公式は物凄く重要で、以後、度々登場します。 使わないと解け 三角比・三角関数の公式一覧。 正弦・余弦・加法定理など このページでは、 三角比・ 三角関数 の公式 をまとめています。 予習・復習に役立てていただければ嬉しいです。 三角比の相互関係 直角三角形と三角比の対応は下の図の通りでしたね。 これから、 y = rsinθ y = r sin ⁡ θ と x = rcosθ x = r cos ⁡ θ という式が得られます。 ちなみに、 y = sinθr y = sin ⁡

高校数学 数 ７７ 三角比 公式編 Youtube

高校数学 三角関数の積分 三角関数の相互関係の利用 受験の月

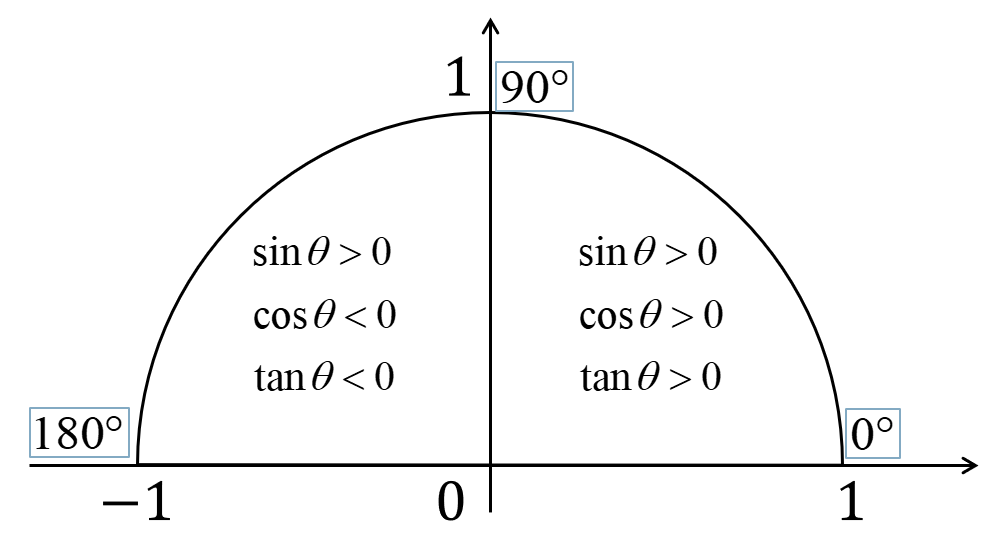
三角関数の相互関係は必ず押さえておきたい重要な公式です。 三角形の相互関係 \(\sin^{2} \theta\cos^{2} \theta=1\) \(\displaystyle \tan \theta=\frac{\sin \theta}{\cos \theta}\) みなさん、こんにちは。「＋αで学びたい高校数学のnote塾」支配人のゆーです。 本日は高校1年生で学習する「三角比の相互関係」について学習していきたいと思います。 sin , cos , tan のうちどれか1つの値でもわかっていれば他の値も求められるという三角比の結びつきを表している公式重要公式「sin 2 θ＋cos 2 θ＝1」を使おう 公式 「sin 2 θ＋cos 2 θ＝1」 を使って、まずはcosθを求めるよ。 解答を書くとき、問題文の 「θは鋭角」 という情報をもとに、 「0°＜θ＜90°より」 と、一言添えよう。 「え？ なんで？ 」と思うかも知れないけれど、驚くべきことに、 「三角比は、角度によってマイナスの値になる場合がある」 んだ。 ただ、マイナスの

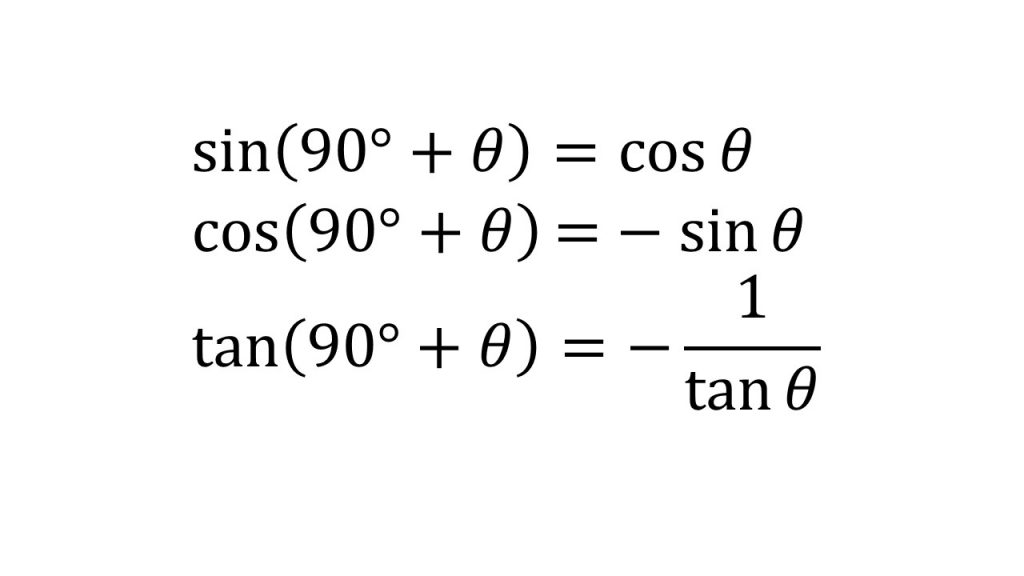
三角比公式 大学受験の王道

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

三角関数の定義 より， sinθ= y r sin θ = y r ， cosθ= x r cos θ = x r ， tanθ = y x tan θ = y x三角比・平面図形公式マインドマップ 三角比の定義，相互関係 a c I 拡張 b tan(90 P(cos ;sin ) 単位円 1 1 x y O O P sin cos 8三角関数の諸公式の「図による証明」 （鋭角 に対する）三角比の基本関係式 ただし， ，， などの角の大きさには制限がつく。 (2)一般的に，三角関数の相互関係sin2 cos2 = 1 は「三平方の定理」から導出する。また，その他の諸公

三角比の相互関係 公式３つの覚え方と使い方は 数スタ

Tanの値からcosの値を求めるときの分数の式変形について 数学 苦手解決q A 進研ゼミ高校講座

 三角比の相互関係って公式丸暗記している人は数学Ⅱで地獄かも→対策 年3月22日 三角比が嫌いになるのは公式が多すぎるからだという意見があります。 逆に考えるとそれを防げば三角比で脱落してしまう人を減らせるかも知れない。 全過去問で数検1三角比90°＋θの公式高校数学Ⅰ 三角比の方程式（正接tan）高校数学Ⅰ 直線の傾きと正接tan高校数学Ⅰ 三角比の相互関係（sin，cosから）高校数学Ⅰ 三角比の相互関係の公式とは次の3つの式です。 三角比の相互関係 ・\( \displaystyle \large{ \color{red}{ \tan \theta = \frac{\sin \theta}{\cos \theta} } } \cdots ① \)

三角比の相互関係の基本問題 Sin8 1 2のとき Cos8の値を求めよ で 高校 教えて Goo

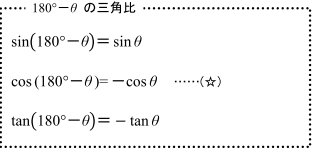
180 8の三角比 数学 苦手解決q A 進研ゼミ高校講座

 和積の公式 \displaystyle \sin A \sin B = 2\sin\frac {A B} {2}\cos\frac {A − B} {2} \displaystyle \sin A − \sin B = 2\cos\frac {A B} {2}\sin\frac {A − B} {2} \displaystyle \cos A \cos B = 2\cos\frac {A B} {2}\cos\frac {A − B} {2} \displaystyle \cos A − \cos B = −2\sin\frac {A B} {2}\sin\frac {A − B} {2}現在地 と前後の項目 高校数学Iで登場する「三角比の相互関係」とは、次の2つの公式のことです。 sin 2 Acos 2 A=1 (1) sinAcosAnnnn (2) 三角比 sinA , cosA , tanA のうち1つ分かれば、残りはこれらの公式を使って「芋づる式に」求まります。 例えば、 sinA がTanA と他の三角比との関係 sin 2 A cos 2 A = 1 の両辺を sin 2 A で割ると (1) より、 cos A sin A = 1 tan A 1 cos 2 A sin 2 A = 1 sin 2 A ⇔ 1 1 tan 2 A = 1 sin 2 A sin 2 A cos 2 A = 1 の両辺を cos 2 A で割ると (1) より、 sin A cos A = tan A sin 2 A cos 2 A 1 = 1 cos 2 A ⇔ tan 2 A 1 = 1 cos 2 A

3

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

 3 三角比の相互関係 この三角比の相互関係の公式は、超重要公式です 。必ず覚えましょう。 公式が成り立つ理由や詳しい解説は「数学Ⅰ三角比sin cos tanの相互関係と覚え方」の記事でまとめているので、ぜひ参考にしてください。 三角比の相互関係 今まで特殊な角度についての三角比を上げてきましたが、 もちろん全ての角度に対して三角比は計算できます 。 なぜなら欲しい三角比の角度をもつ直角三角形を用意して、計算すればいいのですから。 ですが、高校数学の問題では 三角比の相互関係式のまとめ 三角比の相互関係式の証明はそれほど難しくないので、三角比の定義さえ知っていれば理解できたかと思います。 これらの式は、三角比に関する問題を解く上での 基本中の基本 となりますので、 まずはこれら3つの式をしっかりおさえておきましょう。 三角比三角比のまとめ B!

C09 90 0 Sin Cos Lihat Cara Penyelesaian Di Qanda

三角関数 の基本的な定理とその有用性を再確認してみませんか その２ 加法定理 二倍角 三倍角 半角の公式等 ニッセイ基礎研究所

○　高校数学Ｉで登場する「三角比の相互関係」とは、次の２つの公式のことです。 sin 2 A cos 2 A=1 (1) 三角比の相互関係 上で取り決めた3つの三角比に相互に成り立つ関係式がある： $\sin^2 \theta \cos^2 \theta = 1$ $\tan \theta = \frac{\sin \theta}{\cos \theta}$ $1 \tan^2 \theta = \frac{1}{ \cos^2 \theta}$今までの3つの公式に加えて，以下の公式も三角関数の相互関係と呼ばれることがあります： 1 1 tan ⁡ 2 θ = 1 sin ⁡ 2 θ 1\dfrac{1}{\tan^2\theta}=\dfrac{1}{\sin^2\theta} 1 tan 2 θ 1 = sin 2 θ 1

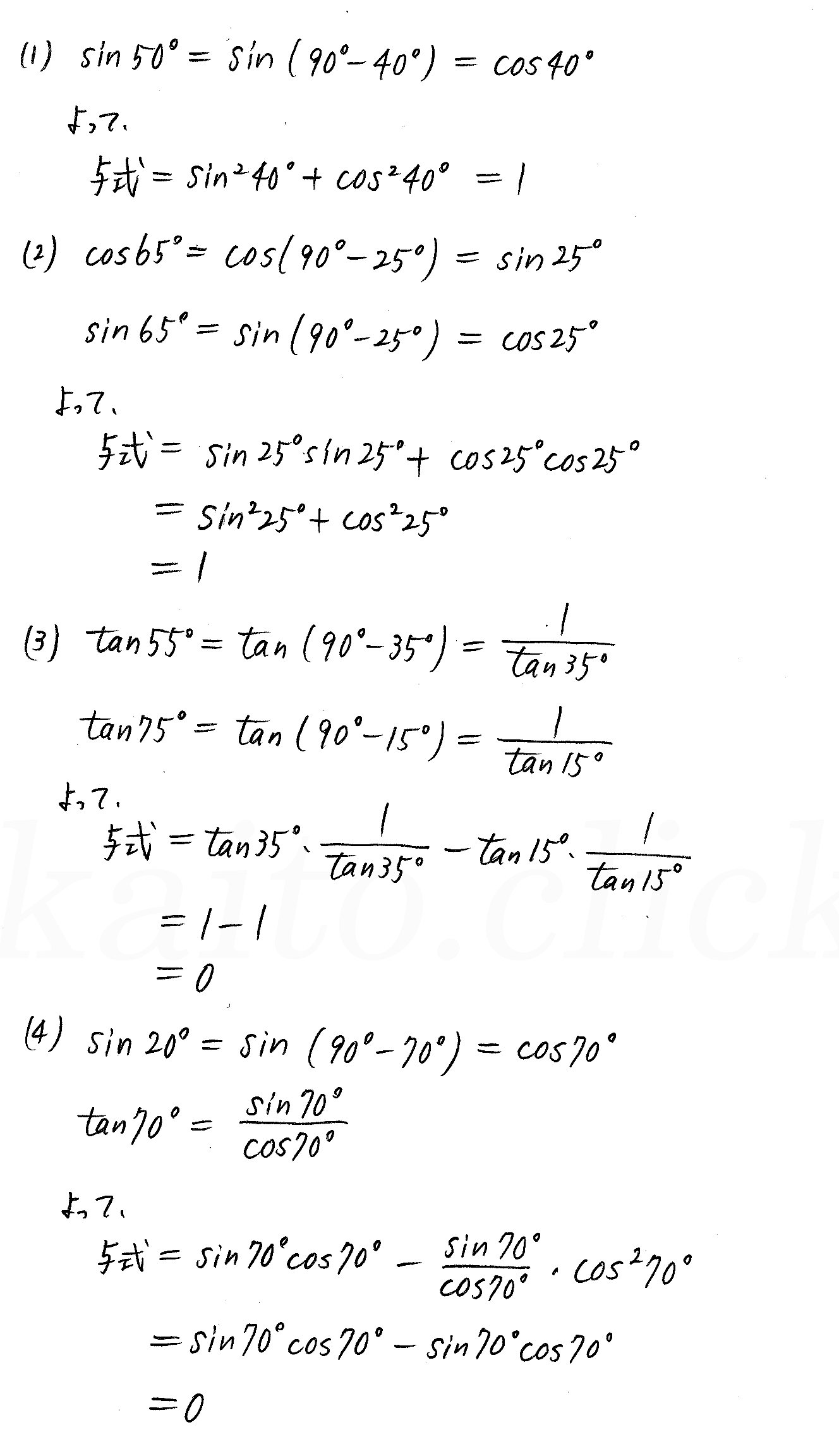
三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

高校数学 三角関数の相互関係 の公式とその証明 Enggy

数学 三角比の式の値を求めよ 隠れた条件を見落とすな 数スタ

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 21年3月16日 エキサイトニュース 5 7

相互関係を 図で解いちゃダメ は正しいか 怜悧玲瓏 高校数学を天空から俯瞰する

48s96ub7b0z5f Net Sankakukansuu Koushiki

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 21年3月16日 エキサイトニュース 5 7

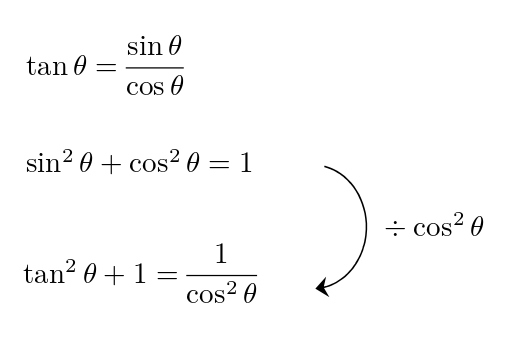
高校数学 三角比 公式一覧 変換 正弦定理 余弦定理 面積 学校よりわかりやすいサイト

高校数学 三角比の相互関係1 図の利用 映像授業のtry It トライイット

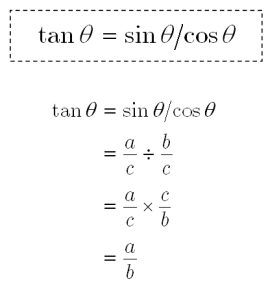
三角比 三角比の相互関係 大人が学び直す数学

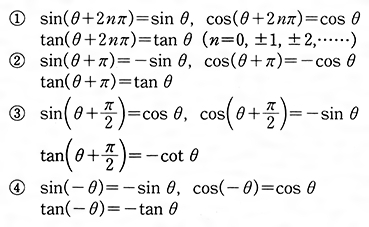
三角関数とは コトバンク

三角比 の重要公式 証明もしっかり解説 Rikeinvest

数学ia 三角比の相互関係 大学入試数学の考え方と解法

山と数学 そして英語 三角比の相互関係の公式 覚えましょう

三角関数の加法定理 倍角公式の利用 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信

三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説

三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要

三角比 三角関数 思考力を鍛える数学

三角比の相互関係とその使い方 高校数学の知識庫

三角比完全網羅 三角比 Sinとcosとtanの定義 覚え方 性質 定理 公式 合格サプリ

今 三角比の相互関係をやっているのですが公式の見分け方 が分かりません 簡単に見分け Clear

三角比は1時間で解けるようになる 外資系コンサルタントが主夫になったら

三角比の相互関係の公式は覚えているのですが 何故上の直角三角形の Yahoo 知恵袋

三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

三角関数 Wikipedia

三角比の相互関係 高校数学の無料オンライン学習サイトko Su

三角比の相互関係 Jsciencer

公式 三角比の相互関係式について 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開

48s96ub7b0z5f Net Sankakuhi Sougo

三角比と三角関数の公式の整理と歴史的背景 単元まとめ ますだ先生の数学の授業で自由に楽しむサイト

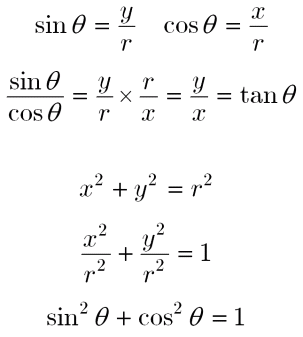
三角比 三角関数の相互関係と 象限 大人が学び直す数学

三角関数の相互関係

公式証明道場２ 三角比の相互関係 数学 Aで学びたい高校のnote塾 Note

三角比を用いた計算問題をマスターしよう スタディクラブ情報局

数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ

Studydoctor三角比の相互関係と計算 高校数学 Studydoctor

三角比まとめ 完全攻略

三角比 ２ 三角比の相互関係 数 A 東大数学9割のkatsuyaが販売する高校数学の問題集

三角関数とは コトバンク

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ

三角比公式 大学受験の王道

三角関数の公式一覧

三角関数 Wikipedia

数学 鈍角での三角比の相互関係の公式の使い方とコツ ページ 2 教科書より詳しい高校数学

3

三角比の相互関係の問題下の公式を使わずに三平方の定理を使って解くのはアリな Yahoo 知恵袋

高校数学 90 8の三角比 映像授業のtry It トライイット

Studydoctor三角関数の式と値 高校数学 Studydoctor

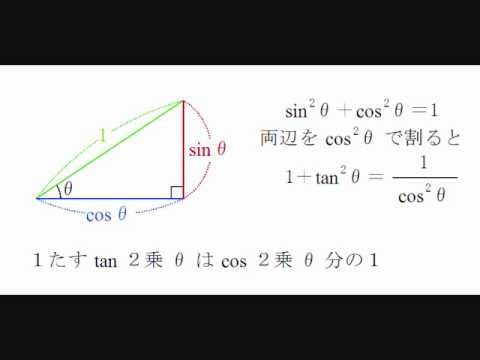
歌って覚える三角比 ２ 三角比の相互関係 Youtube

三角関数の相互関係 大学受験の王道

高校数学 三角関数の相互関係を用いる証明 映像授業のtry It トライイット

高校数学無料問題集 数 第３章 図形と計量 三角比の拡張と相互関係の式 桝 ます Note

三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

怜悧玲瓏 高校数学を天空から俯瞰する

26 三角比の相互関係 正接の解き方と 27 Clear

三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

三角比の相互関係 問題 Youtube

シンコスタン 咲塾

基本 三角比の相互関係 鈍角 なかけんの数学ノート

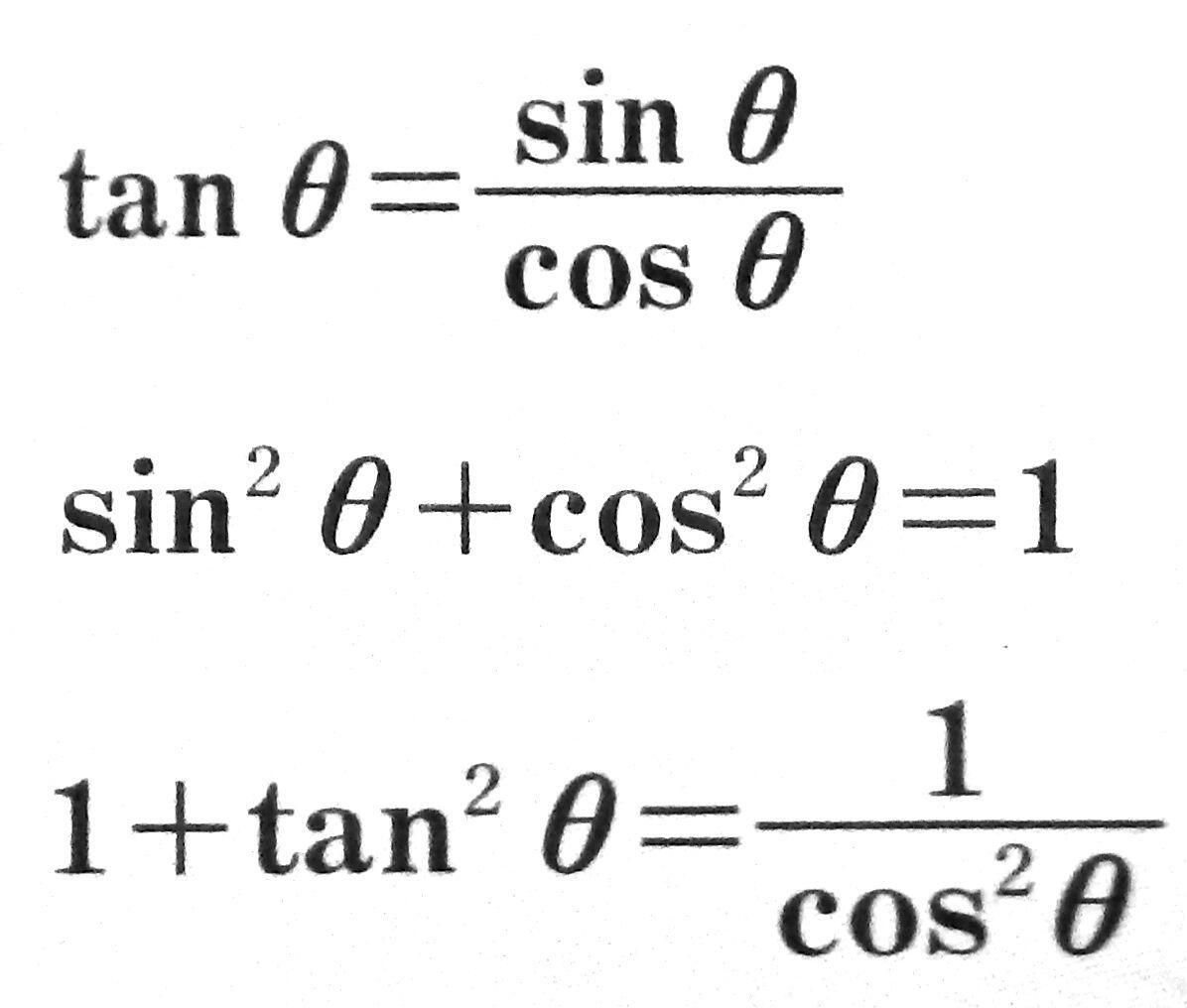
画像でわかる高校数学bot V Tvittere 三角比 三角比の相互関係 T Co Oerqbx2bmb

三角比の相互関係の公式４つって 証明 覚え方 応用問題６選を解説 遊ぶ数学

数学 鈍角での三角比の相互関係の公式の使い方とコツ 教科書より詳しい高校数学

三角比 入門編 Sin Cos Tanって何 90 8 の公式も ますますmathが好きになる 魔法の数学ノート

数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ

数学 三角比 Sin Cos Tanの相互関係と覚え方 理系ラボ

この三角比の相互関係の公式を簡単に覚えれる方法はないですか そんな Yahoo 知恵袋

三角比の公式 鋭角のとき 数学i By Okボーイ マナペディア

三角関数の相互関係とその証明 高校数学の美しい物語

図形と計量 三角比の相互関係について その２ 日々是鍛錬 ひびこれたんれん

Studydoctor三角関数 比 の性質と公式 高校数学 Studydoctor

基本 三角比の相互関係 なかけんの数学ノート

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

高校数学 A 三角比 三角比の相互関係 Sin Cos Tanの三角関係 やはり俺の考察ブログはまちがっている アニメ 数学

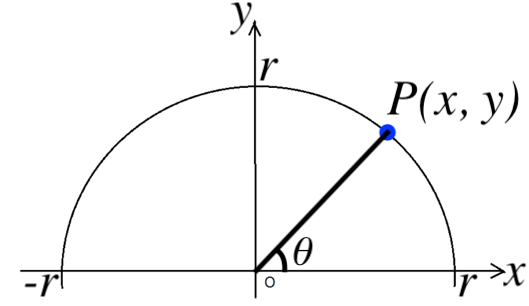
三角比を用いた計算問題をマスターしよう スタディクラブ情報局

図形と計量 三角比の相互関係について その１ 日々是鍛錬 ひびこれたんれん

3倍角の公式の覚え方をマスターしよう 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学

高校数学 三角関数の相互関係と還元公式 負角の公式 補角の公式 余角の公式 受験の月

3倍角の公式の覚え方 ゴロ 自宅を自習室に 医進館に

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

3

高校数学 鈍角を含む三角比の相互関係1 図の利用 映像授業のtry It トライイット

三角比の相互関係 数学 のブログ

1

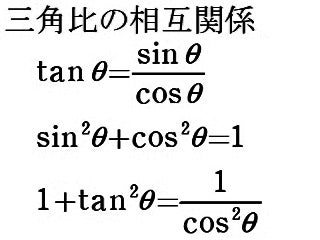
三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

わかりやすい三角比と基本公式 Irohabook

Incoming Term: 三角比の相互関係の公式, 三角比の相互関係の公式 覚え方,